【模板】最大流Dinic+多路增广+当前弧优化

给定指定的一个有向图，其中有两个特殊的点源S(Sources)和汇T(Sinks)，每条边有指定的容量(Capacity)，求满足条件的从S到T的最大流(MaxFlow)。

2018-04-08 已更新

在刚学图论的时候，网络流问题真的让我无从下手，后来找时间研究了一下，发现最大流并不难求

由于给定了一个图，那最大流肯定是定下来的。我们想求最大流，就可以按照二分图匹配的思想，先求可行流，然后增广。

所以我们先写一个增广函数：

int dfs(int now, int res) {
  if(now == end) {
    return res;
  }
  for(int edg = first[now]; edg != -1; edg = edge[edg].next) {
    if(edge[edg].flow <= 0) continue;
    int add = dfs(edge[edg].to, std::min(res, edge[edg].flow));
    if(add > 0) {
      edge[edg].flow -= add;
      return add;
    }
  }
  return 0;
}

long long maxFlow() {
  long long res = 0;
  while(int add = dfs(start, 0x7fffffff)) {
    res += add;
  }
  return res;
}

但是很明显，在一个图中DFS并不是一个优秀的做法，我们需要优化。

启发式

A*的基础思想告诉我们，尝试启发式搜索也许是个好主意。那我们不仿试一试。

如何启发？

从起点开始BFS一遍，试图把图当成分层图（然而并不是），让DFS一层一层走，一直增广到不能再增广了，就可以结束了。

bool setDepth() {
  std::queue<int> que;
  while(!que.empty()) que.pop();
  memset(depth, 0, sizeof(depth));
  depth[start] = 1;
  que.push(start);
  while(!que.empty()) {
    int now = que.front();
    que.pop();
    for(int edg = first[now]; edg != -1; edg = edge[edg].next) {
      if(edge[edg].flow > 0 && depth[edge[edg].to] == 0) {
        depth[edge[edg].to] = depth[now] + 1;
        que.push(edge[edg].to);
      }
    }
  }
  return depth[end] != 0;
}

int dfs(int now, int res) {
  if(now == end) {
    return res;
  }
  for(int edg = first[now]; edg != -1; edg = edge[edg].next) {
    if(depth[edge[edg].to] != depth[now] + 1) continue;
    if(edge[edg].flow <= 0) continue;
    int add = dfs(edge[edg].to, std::min(res, edge[edg].flow));
    if(add > 0) {
      edge[edg].flow -= add;
      return add;
    }
  }
  return 0;
}

long long maxFlow() {
  long long res = 0;
  while(setDepth()) {
    while(int add = dfs(start, 0x7fffffff)) {
      res += add;
    }
  }
  return res;
}

然后我们兴致勃勃地把这篇代码套上主函数交到了OJ上，发现WA了。

![](/images/000.jpg)

为什么会WA？
想一下这样增广真的对吗
当我们遇到下面这种情况的话会怎样：

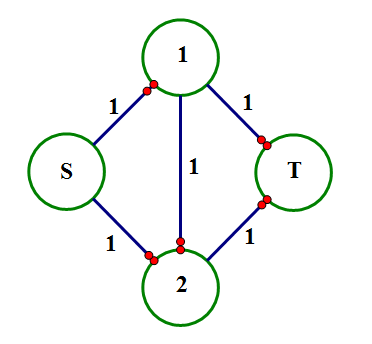
正常情况下，我们先走S->1->T，再走S->2->T，答案正好是2。但是要是一不小心误入歧途，走了S->1->2->T，接下来就无路可走了。

为了避免这种情况，我们要为自己预备一些后悔药，防止自己走错路：建流量为0的反向边，当正边流量减少时，反边流量增加。

//链式前向星存图
void addEdge(int from, int to, int flow) {
  static int cnt = -1;
  edge[++cnt].to = to;
  edge[cnt].flow = flow;
  edge[cnt].next = first[from];
  first[from] = cnt;
  edge[++cnt].to = from;
  edge[cnt].flow = 0;
  edge[cnt].next = first[to];
  first[to] = cnt;
  return;
}

我们以 0index 来存边，那么一个边的反向边就是它自己 ^ 1，也方便了我们找反向边。

所以DFS时的更新流量操作也要改一下

int add = dfs(edge[edg].to, std::min(res, edge[edg].flow));
if(add > 0) {
  edge[edg].flow -= add;
  edge[edg ^ 1].flow += add;
  return add;
}

好的，现在我们整理一下，交到洛谷上

AC!

交到LOJ上喜加一！

emmmmmmm……

为什么会这样呢

然后我翻了下红书，发现maxFlow函数并不是我这么写的，而是这样

long long maxFlow() {
  long long res = 0;
  while(setDepth()) {
    res += dfs(start, 0x7fffffff);
  }
  return res;
}

比我的少了一个while循环。我试图理解了一下，这样写确实比我的写法要更优，所以换上这个再交一发：

AC!

请注意，红书上DFS也与我不一样，这一点在文章结尾已更新

最后放上整份代码：

//LOJ101，未封装
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>

const int MAX_NODE_NUM = 100;
const int MAX_EDGE_NUM = 5000;

struct Edge {
  int to;
  int flow;
  int next;
} edge[(MAX_EDGE_NUM << 1) + 1];

int first[MAX_NODE_NUM + 1];
int depth[MAX_NODE_NUM + 1];
int start;
int end;

void addEdge(const int, const int, const int);
long long maxFlow();

int main() {
  //init
  memset(first, -1, sizeof(first));
  int noden;
  int edgen;
  scanf("%d%d%d%d", &noden, &edgen, &start, &end);
  while(edgen--) {
    int from, to, flow;
    scanf("%d%d%d", &from, &to, &flow);
    addEdge(from, to, flow);
  }
  ///init

  //solve&print
  printf("%lld\n", maxFlow());
  ///solve&print
}

inline void addEdge(const int from, const int to, const int flow) {
  static int cnt = -1;
  edge[++cnt].to = to;
  edge[cnt].flow = flow;
  edge[cnt].next = first[from];
  first[from] = cnt;
  edge[++cnt].to = from;
  edge[cnt].flow = 0;
  edge[cnt].next = first[to];
  first[to] = cnt;
  return;
}

bool setDepth() {
  std::queue<int> que;
  while(!que.empty()) que.pop();
  memset(depth, 0, sizeof(depth));
  depth[start] = 1;
  que.push(start);
  while(!que.empty()) {
    int now = que.front();
    que.pop();
    for(int edg = first[now]; edg != -1; edg = edge[edg].next) {
      if(edge[edg].flow > 0 && depth[edge[edg].to] == 0) {
        depth[edge[edg].to] = depth[now] + 1;
        que.push(edge[edg].to);
      }
    }
  }
  return depth[end] != 0;
}

int dfs(int now, int res) {
  if(now == end) {
    return res;
  }
  for(int edg = first[now]; edg != -1; edg = edge[edg].next) {
    if(depth[edge[edg].to] != depth[now] + 1) continue;
    if(edge[edg].flow <= 0) continue;
    int add = dfs(edge[edg].to, std::min(res, edge[edg].flow));
    if(add > 0) {
      edge[edg].flow -= add;
      edge[edg ^ 1].flow += add;
      return add;
    }
  }
  return 0;
}

long long maxFlow() {
  long long res = 0;
  while(setDepth()) {
    res += dfs(start, 0x7fffffff);
  }
  return res;
}

//luogu最大流，半封装
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
using std::queue;
using std::min;

const int MAX_NODE_NUM = 10000;
const int MAX_EDGE_NUM = 100000;

class NetworkFlow {
 private:
  bool MakeDepth();
  int Dfs(int, int);
  int cnt;
  int start;
  int end;
  int first[MAX_NODE_NUM + 1];
  int depth[MAX_NODE_NUM + 1];
  int to[MAX_EDGE_NUM << 1 | 1];
  int flow[MAX_EDGE_NUM << 1 | 1];
  int next[MAX_EDGE_NUM << 1 | 1];
 public:
  NetworkFlow(int = 0, int = 0);
  void AddEdge(int, int, int);
  int MaxFlow();
};

NetworkFlow::NetworkFlow(int from, int to)
 : start(from), end(to), cnt(-1) {
  memset(first, -1, sizeof(first));
  memset(NetworkFlow::to, 0, sizeof(NetworkFlow::to));
  memset(flow, 0, sizeof(flow));
  memset(next, -1, sizeof(next));
  return;
}

void NetworkFlow::AddEdge(int from, int to, int flow) {
  ++cnt;
  NetworkFlow::to[cnt] = to;
  NetworkFlow::flow[cnt] = flow;
  next[cnt] = first[from];
  first[from] = cnt;
  ++cnt;
  NetworkFlow::to[cnt] = from;
  NetworkFlow::flow[cnt] = 0;
  next[cnt] = first[to];
  first[to] = cnt;
  return;
}

bool NetworkFlow::MakeDepth() {
  queue<int> que;
  memset(depth, 0, sizeof(depth));
  depth[start] = 1;
  que.push(start);
  while(!que.empty()) {
    int now = que.front();
    que.pop();
    for(int nxt = first[now]; nxt != -1; nxt = next[nxt]) {
      if(flow[nxt] > 0 && depth[to[nxt]] == 0) {
        depth[to[nxt]] = depth[now] + 1;
        que.push(to[nxt]);
      }
    }
  }
  if(depth[end] == 0) {
    return 0;
  }
  return 1;
}

int NetworkFlow::Dfs(int now, int res) {
  if(now == end) return res;
  for(int nxt = first[now]; nxt != -1; nxt = next[nxt]) {
    if(depth[to[nxt]] != depth[now] + 1) continue;
    if(flow[nxt] <= 0) continue;
    int d = Dfs(to[nxt], min(res, flow[nxt]));
    if(d > 0) {
      flow[nxt] -= d;
      flow[nxt ^ 1] += d;
      return d;
    }
  }
  return 0;
}

int NetworkFlow::MaxFlow() {
  int res = 0;
  while(MakeDepth()) {
    res += Dfs(start, 0x7fffffff));
  }
  return res;
}

int main() {
  int edgen;
  int noden;
  int start, end;
  scanf("%d%d%d%d", &noden, &edgen, &start, &end);
  NetworkFlow group(start, end);
  int from, to, flow;
  for(int i = 1; i <= edgen; ++i) {
    scanf("%d%d%d", &from, &to, &flow);
    group.AddEdge(from, to, flow);
  }
  printf("%d\n", group.MaxFlow());
  return 0;
}

2018-04-08更新

日后发现我虽然过了LOJ的普通模板，但是这并不是一个标准写法。正确的写法应该是多路增广，就是一次DFS增广很多条路。

int dfs(int now, int flow) {
  if(now == end) {
    return flow;
  }
  int res = 0;//update
  for(int edg = first[now]; edg != -1; edg = edge[edg].next) {
    if(depth[edge[edg].to] != depth[now] + 1) continue;
    if(edge[edg].flow <= 0) continue;
    int add = dfs(edge[edg].to, std::min(flow, edge[edg].flow));
    //if(add > 0) {//update
      edge[edg].flow -= add;
      edge[edg ^ 1].flow += add;
      flow -= add;//update
      res += add;//update
      if(flow == 0) break;//update
    //}//update
  }
  if(res == 0) depth[now] = 0;//update
  //在此感谢igronemyk大佬为我指出这个卡了我很久的地方
  //这个是用来保证多路增广复杂度的
  return res;//update
}

有变化的地方已经用注释标上了update，应该很好理解，就不赘述了。

在向群里的dalao请教后得知还有个当前弧优化。
加上这个后成功更强地A掉了这道题

当前弧，故名思义，就是当前的弧。

当前弧优化，就是记录一下这个结点目前走到哪条边了，下次走的时候直接从这条边开始走就行。

能砍掉很多无用的时间

代码

可能是VCode的博客

不能吃！/工作联系vcodechina@gmail.com/私人联系vcode28629@qq.com

【模板】最大流Dinic+多路增广+当前弧优化

2018-04-08更新