FFT(forever fast TLE)是个很神奇的东西,可以用 $\rm O(nlogn)$ 的时间复杂度来解决多项式乘法的问题(朴素为 $\rm O(n^{2})$ 。
这里感谢我身边的几位dalao,直接或间接的给我讲了好几遍FFT,让我终于理解了FFT的原理
放出他们的博客
https://blog.csdn.net/ggn_2015/article/details/68922404
https://www.luogu.org/blog/ACdreamer/Fast-Fourier-Transformation
https://blog.csdn.net/WADuan2/article/details/79529900
多项式
我们主要了解多项式的两种表示方法:
系数表示法就是我们最常用的表示法
我们只要用数组存下所有的系数就可以了。用两个系数表示法表示的多项试相乘是 $n^{2}$ 的。(即朴素的高精乘)
我们把多项式看成一个函数,一个n次函数需要n+1个在函数上的点就能确定下来。所以可以用一堆点来表示这个多项式。
如果两个多项式对应的 $x_{i}$ 都相同的话,那么只要 $\rm O(n)$ 的时间复杂度就能求出答案的点值表达了。
好的现在我们的需求就是把系数表示和点值表示相互转化就好了。我会挨个数字代入!
朴素代入肯定不行了,复杂度并没有缩减,常数可能还大一点。
所以我们考虑优雅的代入
优雅的代入
我们在原来的基础上再造两个多项式:
那么很明显, $f(x)=g(x^2)+xh(x^2)$
这样我们求一个x的f(x)就变成nlogn了!
原来好像是O(n)来着。
这样我们就写出了一个假的FFT。

那这个有什么用?
答案是配合虚数与单位根一起食用:
虚数
虚数有关的知识大家在高中学过了,或者在初中应该看过百度百科。就算一点也不了解也没关系,我会把咱们能用到的虚数的知识再来讲一下的:
初中数学告诉我们,根号下一个负数是无意义的。于是一帮闲着没事的数学家哲学家为了天下大一统就想赋予 $\sqrt{-1}$ 实际意义,就强行让 $i=\sqrt{-1}$ ,于是形如a+bi这样的数就被称为虚数(其中a,b为实数且b不为0)。
当时的观念认为这是真实不存在的数字。后来人们发现虚数可对应平面上的纵轴,与对应平面上横轴的实数同样真实。
从小我们一直在学实数,初中老师告诉我们,实数就是数轴上的一个点的坐标。如果要表示平面上点的坐标,那我们就需要一个有序数对(a, b)。后来我们了解到,表示平面上一个点的坐标不仅可以是一个单纯的有序数对,我们可以赋予他更实际的意义,比如向量,还有虚数。
那么我们自己定义一个虚数类(结构体)
struct Complex {
Complex(double real = 0, double imag = 0) : real(real), imag(imag) { }
double real;//实部a
double imag;//虚部b
Complex operator*(const Complex &cmplx) const {
//参照两个二项式乘法并将i^2看为-1
return (Complex){real * cmplx.real - imag * cmplx.imag,
real * cmplx.imag + imag * cmplx.real};
}
Complex operator+(const Complex &cmplx) const {
return (Complex){real + cmplx.real, imag + cmplx.imag};
}
Complex operator-(const Complex &cmplx) const {
return (Complex){real - cmplx.real, imag - cmplx.imag};
}
};
当然你也可以用STL自带的complex,但是那个显然没有手写的快。
我们发现虚数的乘法其实是模长相乘,辐角相加。如果模长为1,那么便只有辐角相加了。于是我们就需要单位根:
单位根
复数 $\omega$ 满足 $\omega^{n}=1$ 称作 $\omega$ 是 $n$ 次单位根
如果我们把所有的8次单位根画出来就是这样的:
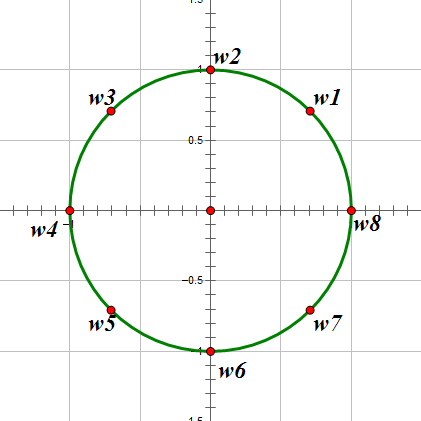
让我们来了解一下单位根的两个性质:
$\omega^{m}_{n}$ 称为n次单位根的m次方
DFT
单位根性质结合刚才的多项式公式,我们可以得到这样的结论
如果在这里你有一些没跟上,可以把之前提到的东西放在一起手推一遍,只要一步就可以得到
我们只要求出每个 $f(\omega^{m}_{\frac{n}{2}})(1\leq m\leq\frac{n}{2})$
就可以轻松求出所有 $f(\omega^{m}_{n})(1\leq m\leq n)$ 了
那么我们递归解决就可以了。
注:多项式的点值表达不一定要用实数,也可以用虚数的点值表达来做。这也就是为什么我们可以FFT。
void DFT(Complex *f, int len) {
if(len == 1) return;
//如果len为1,那么f只有f[0]一个项,无论x为多少f(x)都是f[0],直接返回
Complex *g = new Complex[len >> 1];
Complex *h = new Complex[len >> 1];
for(int i = 0; i < len; i += 2) {
//为g和h分配系数
g[i >> 1] = f[i];
h[i >> 1] = f[i + 1];
}
FFT(g, len >> 1);
FFT(h, len >> 1);
Complex wn(std::cos(2 * Pi / len), std::sin(2 * Pi / len));
//const double PI = std::acos(-1);也可以用cmath的M_PI(我没试过)
//wn为n次单位根
Complex w(1,0);
//w为当前的x
for(int i = 0; i < (len >> 1); ++i) {
//见代码下面的注S
f[i] = g[i] + w * h[i];
f[i + (len >> 1)] = g[i] - w * h[i];
w = w * wn;
}
return;
}
注S:当代码执行到这里时,f[i]表示多项式f的系数 $a_{i}$ ,g[i]表示 $g(\omega^{i}_{\frac{n}{2}})$ ,h[i]参见g[i]。
啊?你问我为啥叫DFT不叫FFT?
因为FFT分为两个部分,把系数表达变为点值表达叫做DFT,变回来叫IDFT。我们目前讲的都是DFT。
FFT这样一来其实就可以了,但是没人这么写,因为既然写了FFT就是为了快,然而递归的常数真的很大,所以考虑非递归版。
非递归版DFT
观察递归过程
0 1 2 3 4 5 6 7
递归一次:
0 2 4 6 1 3 5 7
递归两次:
0 4 2 6 1 5 3 7
递归三次不变。
把他们化为二进制看一眼:
000 100 010 110 001 101 011 111
发现规律!
二进制是从左到右进位的!
所以我们试图直接进入到递归最后一层,然后一点一点往上爬:
void DFT(Complex arr[], int limit) {
for(int i = 0, j = 0; i < limit; ++i) {
//将arr[i]直接变成二进制从左到右进位版本
//后有详解
if(i > j) std::swap(arr[i], arr[j]);
int bin = limit >> 1;
while((j ^= bin) < bin) bin >>= 1;
}
for(int len = 2; len <= limit; len <<= 1) {
//len相当于递归版的len
Complex lenUnitRoot(std::cos(2 * PI / len), sin(2 * PI / len));
//lenUnitRoot: len次单位根
int mid = len >> 1;
for(int i = 0; i < limit; i += len) {
Complex nowX(1, 0);
//当前的x
for(int j = i; j < i + mid; ++j) {
Complex left = arr[j];
Complex right = nowX * arr[j + mid];
arr[j] = left + right;
arr[j + mid] = left - right;
nowX = nowX * lenUnitRoot;
//更新当前的x到下一个x
}
}
}
return;
}
重点讲一下第一个for循环是如何把arr[i]按二进制排序的
你总会在不同人写的FFT里找到不同的方式完成这个事情,比如GGN大佬的变换方式看上去就比较神。然而好像比我的慢点(洛谷评测结果,原因未知)
这是我代码中出现的for循环:
for(int i = 0, j = 0; i < limit; ++i) {
if(i > j) std::swap(arr[i], arr[j]);
int bin = limit >> 1;
while((j ^= bin) < bin) bin >>= 1;
}
我们可以把它展开,变成一个等价操作:
for(int i = 0; i < limit; ++i) {
temp[i + 1] = temp[i];
int bin = limit >> 1;
while(true) {
temp[i + 1] ^= bin;
if(temp[i + 1] < bin) {
bin >>= 1;
} else {
break;
}
}
}
for(int i = 0; i < (limit >> 1); ++i) {
std::swap(arr[i], temp[i]);
}
再展开while循环内:
for(int i = 0; i < limit; ++i) {
temp[i + 1] = temp[i];
int bin = limit >> 1;
while(true) {
int is_one = temp[i + 1] & bin;
temp[i + 1] ^= bin;
if(is_one) {
bin >>= 1;
} else {
break;
}
}
}
for(int i = 0; i < (limit >> 1); ++i) {
std::swap(arr[i], temp[i]);
}
这样一来这个操作就显而易见了!其实就是在模拟加一这个过程。
到这里,DFT终于讲完了。
IDFT
IDFT就是DFTd逆变换,也就是要把点值表示法变回系数表示法。
GGN大佬表示其实就是乘一个逆矩阵,然而我并不明白是啥意思。
因为只需要在DFT里改两处,所以背下来就好了!
能理解固然更好,然而我这里真的找不到能让我理解IDFT的资料。
如果大家想理解IDFT的过程,可以参考我在文章头放的几篇博客,我就不太(会)讲了。
const double PI = acos(-1.0);
const int DFT = 2;
const int IDFT = -2;
void FFT(Complex arr[], int limit, int mode) {
//mode输入DFT或IDFT
for(int i = 0, j = 0; i < limit; ++i) {
if(i > j) std::swap(arr[i], arr[j]);
int bin = limit >> 1;
while((j ^= bin) < bin) bin >>= 1;
}
for(int len = 2; len <= limit; len <<= 1) {
Complex lenUnitRoot(std::cos(2 * PI / len), sin(mode * PI / len));
//mode第一次出现
int mid = len >> 1;
for(int i = 0; i < limit; i += len) {
Complex nowX(1, 0);
for(int j = i; j < i + mid; ++j) {
Complex left = arr[j];
Complex right = nowX * arr[j + mid];
arr[j] = left + right;
arr[j + mid] = left - right;
nowX = nowX * lenUnitRoot;
}
}
}
if(mode == IDFT) {
//逆变换需要除以limit,然后四舍五入避免精度误差
for(int i = 0; i < limit; ++i) {
arr[i].real = int(arr[i].real / limit + 0.5);
arr[i].imag = 0;// 为了美观加上的一句话,没用
}
}
return;
}