$e=1.602\times10^{-19}C$
$q=ne,n=1,2,3,…$
单位:库仑(C)
库仑定律:
$F=k\frac{q_1q_2}{r^2}=\frac{1}{4\pi\varepsilon_0}\frac{q_1q_2}{r^2}$
$k=\frac{1}{4\pi\varepsilon_0}=9\times10^9 Nm^{-2}C^{-2}$
$\varepsilon_0$ 为真空中的介电常数,为 $8.85\times10^{-12}N^{-1}m^2C^{-2}$
矢量形式: $\vec{F}=\frac{1}{4\pi\varepsilon_0}\frac{q_1q_2}{r^2}\vec{e_r}$ ,表示力的方向
电场强度:$\vec{E}=\frac{\vec{F}}{q}$
点电荷电场强度:$\vec{E}=\frac{q}{4\pi\varepsilon_0r^2}\vec{e_r}$
点电荷系电场强度:$\vec{E}=\sum_{i=1}^n\vec{E}_i=\frac{\vec{F}}{q_0}=\sum_{i=1}^n\frac{\vec{F_i}}{q_0}$
连续带电体:将物体分为多个电荷元
- 线电荷$dq=\lambda\mathrm dl$
- 面电荷$dq=\sigma\mathrm ds$
- 体电荷$dq=\rho\mathrm dv$
点偶极子:大小相等,符号相反且存在一微小间距 $l$ 的两个点电荷构成的复合体
电偶极矩:$\vec{p}=q\vec{l}$
电偶极子延长线上任意一点 A 的场强:
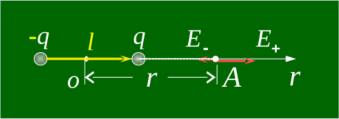
电偶极子中垂线上任意一点 B 的场强:
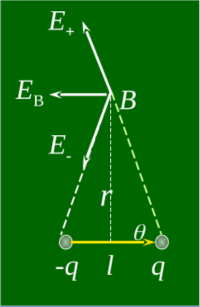
均匀带电棒
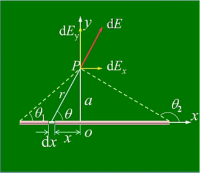
均匀带电直线
高斯定理版:
作高为 $h$ 半径为 $a$ 的圆柱面为高斯面
均匀带电 $q$ 圆环,计算轴线上任一点 $P$ 的场强
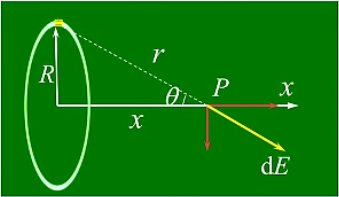
均匀带电圆盘
均匀带电平面
当考察点很接近带电平面时 $x\ll R$ ,可以把带电平面近似看作无限大来处理
$R\ll x$ 时 $E=\frac{q}{4\pi\varepsilon_0x^2}$
静电场中电场线的特点
- 电场线起始于正电荷,终止于负电荷
- 电场线不闭合,不相交
- 曲线上每一点的切线方向表示该点处电场强度的方向
- 电场线密集处电场强,电场线稀疏处电场弱
- 垂直通过单位面积的电场线条数,在数值上就等于该点处电场强度的大小。即:曲线的疏密表示该点处电场强度的大小。 $E=\frac{\mathrm d\Phi_e}{\mathrm dS_\bot}$
电通量
电场强度通量(电通量) $\Phi_e$ :通过电场中任一曲面的电场线条数。
$E=\frac{\mathrm d\Phi_e}{\mathrm dS_\bot}$
$\Phi_e=\vec E\cdot\vec S$
非均匀电场的电通量
$\mathrm d\Phi_e=E\cos\theta\mathrm dS=\vec E\cdot\mathrm d\vec S$
$\mathrm \Phi_e=\int_SE\cos\theta\mathrm dS=\int_S\vec E\cdot\mathrm d\vec S$
对于闭合曲面的电通量: $\Phi_e=\oint_S\vec E\cdot\mathrm d\vec S$ 。规定外法线方向为正
- 当 $\theta\lt90\degree$ 时 $\Phi_e\gt 0$ 。电场线穿出闭合曲面
- 当 $\theta\gt90\degree$ 时 $\Phi_e\lt 0$ 。电场线穿进闭合曲面
- 当 $\theta=90\degree$ 时 $\Phi_e=0$ 。电场线与曲面相切
高斯定理
在真空中静电场内,通过任一闭合曲面的电场强度通量等于该曲面所包围的所有电电荷的代数和的 $\frac1{\varepsilon_0}$ 倍
$\Phi_e=\oint_S\vec E\cdot\mathrm d\vec S=\left\{\begin{aligned}&=\frac1{\varepsilon_0}\sum q_i&\text{(分立)}\\&=\frac1{\varepsilon_0}\int\mathrm dq&\text{(连续)}\end{aligned}\right.$
$\sum q_i$ 表示高斯面内电荷的代数和
关于高斯定理的说明:
- 高斯定离是反映静电场性质(有源性)的一条基本定理
- 高斯定理是在库仑定律的基础上得出的,但它的应用范围比库仑定律更为广泛
- 高斯定理反映闭合曲线内电荷代数和与电通量关系,不是与电场强度关系
- 若高斯面内的电荷的电量为零,则通过高斯面的电通量为零,但高斯面上各点的电场强度并不一定为零
- 通过任意闭合曲面的电通量只决定于它所包围的电荷的代数和,闭合曲面外的电荷对电通量无贡献。但电荷的空间分布会影响闭合面上各电处的场强大小和方向
- 高斯定理中所说的闭合曲面,通常称为高斯面
高斯定理的应用——求电场强度
高斯定理计算电场强度的条件:
- 带电体的电场强度分布要具有高度对称性
- 高斯面上的电场强度大小处处相等
- 面积元 $\mathrm dS$ 的法线方向与该处的电场强度的方向一致
均匀带电球体场强分布
点在球体外:
点在球体内:
无限长带电圆柱面,单位长度带电 $\lambda$
柱面内: $E=0$
柱面外:
无限长均匀带电圆柱体
柱面内:
柱面外:
无限大均匀带电平面
两无限大带异号电荷平面的场强分布
两平面之间:
两平面外侧:
静电场环路定理
静电场的保守性
静电场力作功的特点:与路径无关
在点电荷 $q$ 的电场中移动 $q_0$ 由 $a\rightarrow b$ 的过程中,电场力 $F=qE$ ,对 $q_0$ 作的功:
所以试验电荷在静电场中移动时,电场力作用的功只与试验电荷的起点和终点的位置有关,与路径无关。即电场力是保守力,静电场是保守场。
静电场的环路定理
在静电场中,沿闭合回路移动 $q_0$ 电场力做的功为 $0$
静电场的环路定理:静电场中电场强度沿任意闭合路径的线积分(称 $\vec E$ 的环流)为 $0$
环路定理的意义
- 静电场是保守场(无旋场)
- 静电场力是保守力,做功与路径无关
- 环路定理要求电场线不能闭合
结论: $\vec E$ 遵守高斯定理和环路定理说明静电场是有源保守场。
电势能
保守力做功等于势能的减少
令 $b$ 点的势能为零,则 $a$ 点的电势能 $E_{pa}=\int_a^bq_0\vec E\cdot\mathrm d\vec l$
结论: 试验电荷 $q_0$ 在空间某处的电势能在数值上就等于将 $q_0$ 从该处移至势能的零点电场力所做的功
注意:
- 对于有限带电体,一般取无限远为势能零点
- 对于无限大带电体,常取有限远为势能零点
- 实际问题时常取大地、仪器外壳等为势能零点
- 电势能为电场和位于电场中的电荷这个系统所有
- 电势能是标量,可正可负
电势差和电势
电势 $V_a=\frac{E_{pa}}{q_0}=\int_a^\infty\vec E\cdot\mathrm d\vec l$
单位:伏特 $V=JC^{-1}$
电势的意义:电场中 $a$ 点的电势在数值上等于把单位正电荷从 $a$ 点移至势能零点处电场力所作的功
电势差: $V_{ab}=V_a-V_b=\int_a^b\vec E\cdot \mathrm d\vec l$
静电场中 $a$ , $b$两点的电势差,等于将单位正电荷从 $a$ 点移至 $b$ 点电场力所作的功
点电荷场中的电势
$V_a=\frac q{4\pi\varepsilon_0r_a}$
均匀带电球体的电势
由高斯定理求出电场强度分布
当 $r\le R$时
当 $r\gt R$ 时
求无限长均匀带电直线外任一点 $P$ 的电势,电荷密度 $\lambda$
若取零势能点 $r_0=1(m)$ ,则 $V=\frac{-\lambda}{2\pi\varepsilon_0}\ln r$
均匀带电圆环上一点的电势

可以使用定义法求电势,但更好的是使用叠加法
等势面 电势梯度
- 沿等势面移动电荷,电场力不做功
- 等势面处处与电场线正交
- 等势面稠密处电场强度大
电场强度与电势梯度的关系
结论:电场中给定点的电场强度沿某一方向的分量等于这一点电势沿该方向变化率的负值。
电势梯度 $\nabla V$ 的大小等于电势在该点最大空间变化率;方向沿等势面法向,指向电势增加的方向。
$\nabla V=\frac{\partial V}{\partial x}\vec i+\frac{\partial V}{\partial y}\vec j+\frac{\partial V}{\partial z}\vec k$
静电场小结
计算电势的方法
- 点电荷场的电势及叠加原理
$V=\int\frac{\mathrm dq}{4\pi\varepsilon_0r}$
- 根据电势的定义
$V_p=\int_p^{\text{0势能点}}\vec E\mathrm d\vec l$
- 电势差
$V_{ab}=V_a-V_b=\int_a^b\vec E\mathrm d\vec l$
计算场强的方法
- 点电荷场的场强及叠加原理
$\vec E=\int\frac{\vec r\mathrm dq}{4\pi\varepsilon_0r^3}$
- 电势梯度
$-\nabla V=\vec E$
- 高斯定理
$\Phi_e=\oint_S\vec E\mathrm d\vec S=\frac 1{\varepsilon_0}\iiint_\Sigma \mathrm dq$
两个基本定理:
- 高斯定理
- 环路定理
主要公式
点电荷的场强 $E=\frac q{4\pi\varepsilon_0r^2}$ 和电势 $V=\frac q{4\pi\varepsilon_0 r}$
均匀带电球面的场强 $E=\left\{\begin{aligned}&\frac q{4\pi\varepsilon_0r^2}&(r\ge R)\\&0&(r\le R)\end{aligned}\right.$ 和电势 $V=\left\{\begin{aligned}
&\frac q{4\pi\varepsilon_0r}&(r\ge R)\\&\frac q{4\pi\varepsilon_0R}&(r\le R)
\end{aligned}\right.$无限长均匀带电直线的场强 $E=\frac\lambda{2\pi\varepsilon_0r}$
- 带电圆环轴线上的的场强$E=\frac{qx}{4\pi\varepsilon_0(x^2+R^2)^{\frac32}}$
- 无限大均匀带电平面的场强 $E=\frac\sigma{2\varepsilon_0}$
- 电通量 $\Phi_e=\int_S\vec E\mathrm dS=\int_SE\cos\theta\mathrm dS$
- 静电力的功 $W_{ab}=q_0\int_a^b\vec E\mathrm dl=q_0(V_a-V_b)=q_0V_{ab}$
- 场强与电势的关系 $\begin{aligned}
V_a=\int_a^\infty\vec E\mathrm d\vec l\\
\vec E=-\nabla V=-\frac{\partial V}{\partial n}\vec n_0
\end{aligned}$