导体中的静电平衡

• 导体：存在大量可自由移动的电荷
• 绝缘体：理论上认为一个自由移动的电荷也没有。也称电介质
• 半导体：介于上述两者之间
• 静电感应：在外电场的影响下，导体表面不同部分出现正负电荷的现象
• 静电平衡：导体内部和表面没有电荷的宏观定向运动
• 感应电荷：因静电感应而在导体两侧表面上出现的电荷。

静电平衡时导体中的电场特性：

1. 导体内部场强处处为零/导体为一等势体
2. 表面场强垂直于导体表面/导体表面是一个等势面

将金属球放入均匀电场，电场线向内发生弯曲。电场不再是均匀场

1. 在静电平衡下，导体所在的电荷只能分布在导体的表面，导体内部没有净电荷。（在导体内部使用高斯定理证明）
2. 处于静电平衡的导体，其表面上各点的电荷密度与表面临近处场强的大小成正比。 $E=\frac\sigma{\varepsilon_0}$
3. 静电平衡下的孤立导体，其表面处电荷密度 $\sigma$ 与该表面曲率有关，曲率 $\frac1R$ 越大的地方电荷密度也越大，曲率越小的地方电荷密度也越小。

有导体存在时静电场的分析与计算

空腔导体

1. 腔内无带电体

电荷分布在导体外表面，导体内部和内表面没净电荷。

1. 腔内有带电体

在静电平衡下，电荷分布在导体内、外两个表面，其中内表面的电荷是空腔内带电体的感应电荷，与腔内带电体的电荷等量异号。

静电屏蔽

静电屏蔽：一个接地的空腔导体可以隔离内外电场的影响

1. 空腔导体，腔内没有电荷

空腔导体起到屏蔽外电场的作用

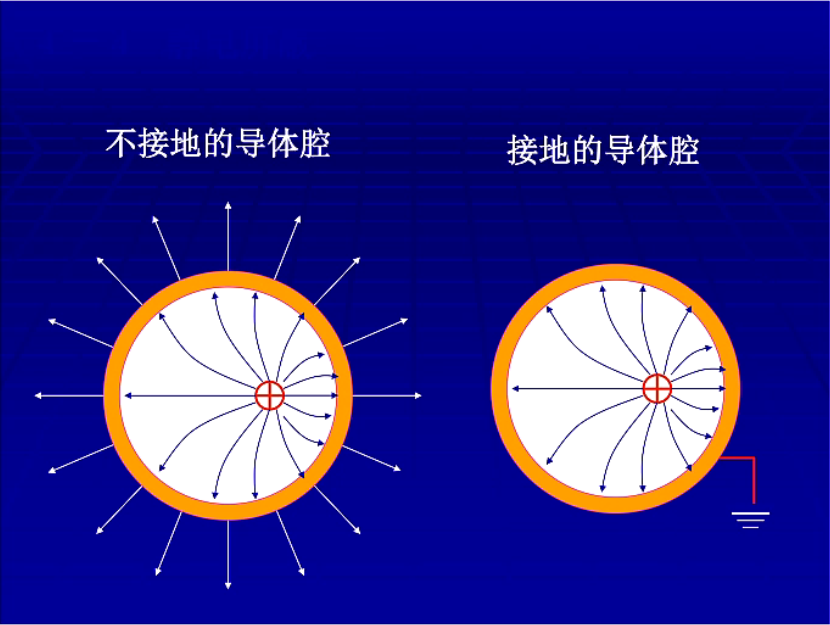
1. 空腔导体，腔内存在电荷

接地的空腔导体可以屏蔽内、外电场的影响

有导体存在时静电场场量的计算原则

1. 静电平衡的条件 $E_\text内=0$ 或 $V=c$
2. 基本性质方程 $\oint_S\vec E\mathrm d\vec s=\frac{\sum_i q_i}{\varepsilon_0}$ ， $\oint_L\vec E\mathrm d\vec l=0$
3. 电荷守恒定率 $\sum_i Q_i=c$

静电场中的电介质

电位移 $\vec D=\varepsilon_0\varepsilon_r\vec E$

电介质中的高斯定理： $\oint_S\vec D\cdot\mathrm d\vec S=\sum\limits_iq_i$

电容和电容器

$$C=\frac qV=\frac q{\int\vec E\mathrm d\vec l}\\$$

并联： $C=\sum C_i$

串联：电荷量相同，即 $C\cdot V$ 相同， $\frac1C=\sum\frac1{C_i}$

平行板电容器： $C=\frac{\varepsilon_0\varepsilon_rS}{d}$

平行板电容器中电位移恒为电荷面密度 $\sigma$

静电场的能量

点电荷系的电能

$$\begin{aligned} W&=q\Delta V\\ &=q\frac{q_0}{4\pi\epsilon_0r} \end{aligned}$$

有多个电荷时，设 $V_i$ 表示除 $q_i$ 外的所有电荷在 $q_i$ 所在点形成的电势

$$W=\frac12\sum_{i=1}^n q_iV_i$$

如果是连续带电体

$$W=\frac12\int_qV\mathrm dq$$

如果只考虑一个带电体，则上式给出的是该带电体的固有能量，或称自能。

电容量的能量

$$\mathrm dW=V\mathrm dq=\frac 1Cq\mathrm dq\\ \begin{aligned} W&=\int_0^Q\frac1Cq\mathrm dq\\ &=\frac12\frac{Q^2}C\\ &=\frac12CV_{AB}^2\\ &=\frac12QV_{AB} \end{aligned}$$

电场的能量

电场的能量密度为 $w_e=\frac12\varepsilon E^2$

电场的总能量为 $\int w_e\mathrm dV$